PROGRAMACION LINEAL CON SOLVER
Antes de ver que es solver y como usarlo, veremos que es el metodo simplex
El Método Simplex es un método analítico de solución de problemas de programación lineal, capaz de resolver modelos más complejos que los resueltos mediante el método gráfico sin restricción en el número de variables.
El Método Simplex es un método iterativo que permite ir mejorando la solución en cada paso. La razón matemática de esta mejora radica en que el método consiste en caminar del vértice de un poliedro a un vértice vecino de manera que aumente o disminuya (según el contexto de la función objetivo, sea maximizar o minimizar), dado que el número de vértices que presenta un poliedro solución es finito siempre se hallará solución.
¿Qué es una matriz identidad?
Una matriz puede definirse como una ordenación rectangular de elementos, (o listado finito de elementos), los cuales pueden ser números reales o complejos, dispuestos en forma de filas y de columnas.
La matriz idéntica o identidad es una matriz cuadrada (que posee el mismo número tanto de columnas como de filas) de orden n que tiene todos los elementos diagonales iguales a uno (1) y todos los demás componentes iguales a cero (0), se denomina matriz idéntica o identidad de orden n, y se denota por:
La importancia de la teoría de matrices en el Método Simplex es fundamental, dado que el algoritmo se basa en dicha teoría para la resolución de sus problemas.
Consideraciones importantes al utilizar el Método Simplex
Variables de holgura y exceso
El Método Simplex trabaja basándose en ecuaciones y las restricciones iniciales que se modelan mediante programación lineal no lo son, para ello hay que convertir estas inecuaciones en ecuaciones utilizando unas variables denominadas de holgura y exceso relacionadas con el recurso al cual hace referencia la restricción y que en el tabulado final representa el «Slack or surplus»al que hacen referencia los famosos programas de resolución de investigación de operaciones, estas variables adquieren un gran valor en el análisis de sensibilidad y juegan un rol fundamental en la creación de la matriz identidad base del Simplex.
Estas variables suelen estar representadas por la letra «S», se suman si la restricción es de signo «<= » y se restan si la restricción es de signo «>=».
Por ejemplo:
Variable artificial / Método de la «M»
Una variable artificial es un truco matemático para convertir inecuaciones «>=» en ecuaciones, o cuando aparecen igualdades en el problema original, la característica principal de estas variables es que no deben formar parte de la solución, dado que no representan recursos. El objetivo fundamental de estas variables es la formación de la matriz identidad.
Estas variables se representa por la letra «A», siempre se suman a las restricciones, su coeficiente es M (por esto se le denomina Método de la M grande, donde M significa un número demasiado grande muy poco atractivo para la función objetivo), y el signo en la función objetivo va en contra del sentido de la misma, es decir, en problemas de Maximización su signo es menos (-) y en problemas de Minimización su signo es (+), repetimos con el objetivo de que su valor en la solución sea cero (0).
Método Simplex paso a paso
El problema
La empresa el SAMÁN Ltda. Dedicada a la fabricación de muebles, ha ampliado su producción en dos líneas más. Por lo tanto actualmente fabrica mesas, sillas, camas y bibliotecas. Cada mesa requiere de 2 piezas rectangulares de 8 pines, y 2 piezas cuadradas de 4 pines. Cada silla requiere de 1 pieza rectangular de 8 pines y 2 piezas cuadradas de 4 pines, cada cama requiere de 1 pieza rectangular de 8 pines, 1 cuadrada de 4 pines y 2 bases trapezoidales de 2 pines y finalmente cada biblioteca requiere de 2 piezas rectangulares de 8 pines, 2 bases trapezoidales de 2 pines y 4 piezas rectangulares de 2 pines. Cada mesa cuesta producirla $10000 y se vende en $ 30000, cada silla cuesta producirla $ 8000 y se vende en $ 28000, cada cama cuesta producirla $ 20000 y se vende en $ 40000, cada biblioteca cuesta producirla $ 40000 y se vende en $ 60000. El objetivo de la fábrica es maximizar las utilidades.

Paso 1: Modelación mediante programación lineal
Variables:
X1 = Cantidad de mesas a producir (unidades)
X2 = Cantidad de sillas a producir (unidades)
X3 = Cantidad de camas a producir (unidades)
X4 = Cantidad de bibliotecas a producir (unidades)
Restricciones:
2X1 + 1X2 + 1X3 + 2X4 <= 24
2X1 + 2X2 + 1X3 <= 20
2X3 + 2X4 <= 20
4X4 <= 16
Función Objetivo:
ZMAX = 20000X1 + 20000X2 + 20000X3 + 20000X4
Paso 2: Convertir las inecuaciones en ecuaciones
En este paso el objetivo es asignar a cada recurso una variable de Holgura, dado que todas las restricciones son «<=».
2X1 + 1X2 + 1X3 + 2X4 + 1S1 + 0S2 + 0S3 + 0S4 = 24
2X1 + 2X2 + 1X3 + 0X4 + 0S1 + 1S2 + 0S3 + 0S4 = 20
0X1 + 0X2 + 2X3 + 2X4 + 0S1 + 0S2 + 1S3 + 0S4 = 20
0X1 + 0X2 + 0X3 + 4X4 + 0S1 + 0S2 + 0S3 + 1S4 = 16
De esta manera podemos apreciar una matriz identidad (n = 4), formado por las variables de holgura las cuales solo tienen coeficiente 1 en su respectivo recurso, por el ejemplo la variable de holgura «S1» solo tiene coeficiente 1 en la restricción correspondiente a el recurso 1.
La función objetivo no sufre variaciones:
ZMAX = 20000X1 + 20000X2 + 20000X3 + 20000X4
Paso 3: Definir la solución básica inicial
El Método Simplex parte de una solución básica inicial para realizar todas sus iteraciones, esta solución básica inicial se forma con las variables de coeficiente diferente de cero (0) en la matriz identidad.
1S1 = 24
1S2 = 20
1S3 = 20
1S4 = 16

Solución: (segundo término)= En esta fila se consigna el segundo término de la solución, es decir las variables, lo más adecuado es que estas se consignen de manera ordenada, tal cual como se escribieron en la definición de restricciones.
Cj = La fila «Cj» hace referencia al coeficiente que tiene cada una de las variables de la fila «solución» en la función objetivo.
Variable Solución = En esta columna se consigna la solución básica inicial, y a partir de esta en cada iteración se van incluyendo las variables que formarán parte de la solución final.
Cb = En esta fila se consigna el valor que tiene la variable que se encuentra a su derecha «Variable solución» en la función objetivo.
Zj = En esta fila se consigna la contribución total, es decir la suma de los productos entre término y Cb.
Cj – Zj = En esta fila se realiza la diferencia entre la fila Cj y la fila Zj, su significado es un «Shadow price», es decir, la utilidad que se deja de recibir por cada unidad de la variable correspondiente que no forme parte de la solución.
Solución inicial:
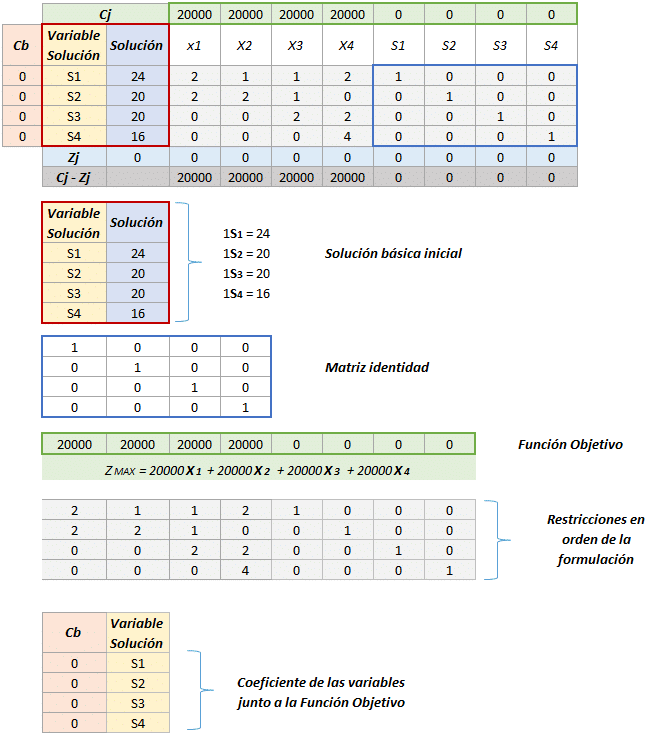
Paso 5: Realizar las iteraciones necesarias
Este es el paso definitivo en la resolución por medio del Método Simplex, consiste en realizar intentos mientras el modelo va de un vértice del poliedro objetivo a otro.
El procedimiento a seguir es el siguiente:
1. Evaluar que variable entrará y cual saldrá de la solución óptima:

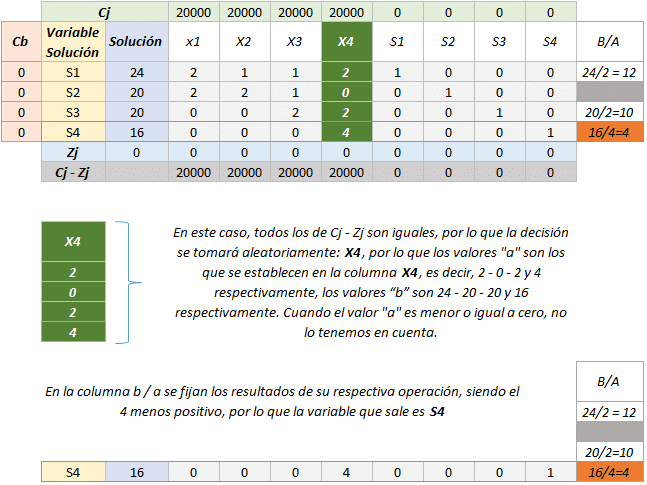
2. El hecho de que una variable distinta forme parte de las variables solución implica una serie de cambios en el tabulado Simplex, cambios que se explicarán a continuación.
- Lo primero es no olvidar el valor del «a» correspondiente a la variables a entrar, en este caso el «a = 4».
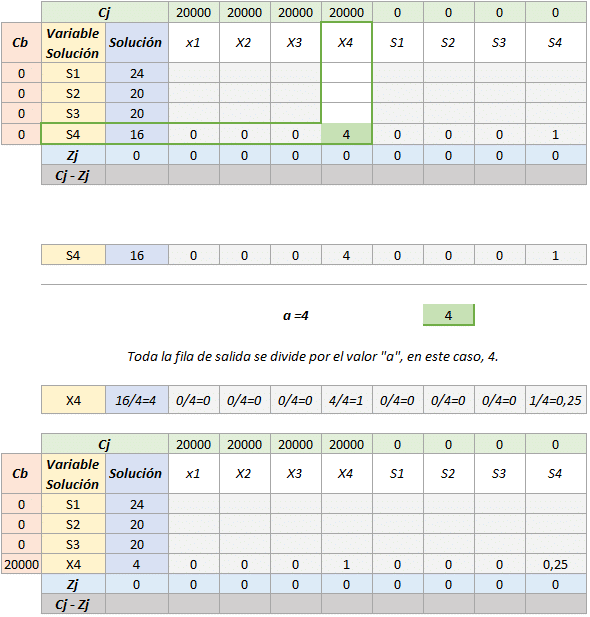
- Lo siguiente es comenzar a rellenar el resto de la tabla, fila x fila.
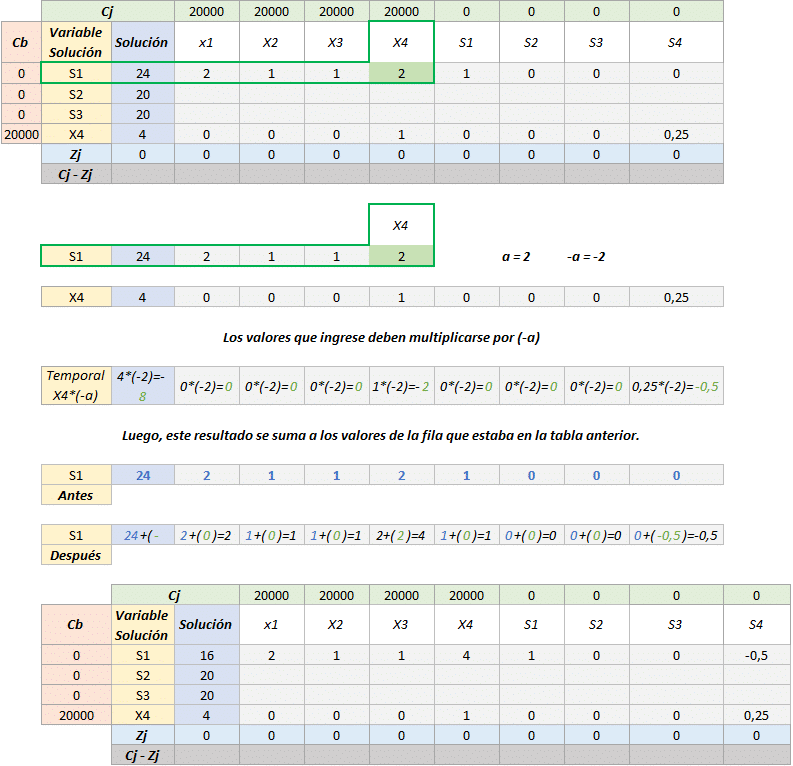
- Se repite este procedimiento con las dos filas restantes, ahora se harán los cálculos correspondientes en el resto de las celdas.
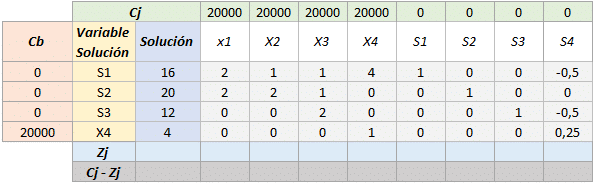
Una vez establecidos los valores de la matriz, puede calcular hasta llenar la tabla correspondiente a la primera iteración.
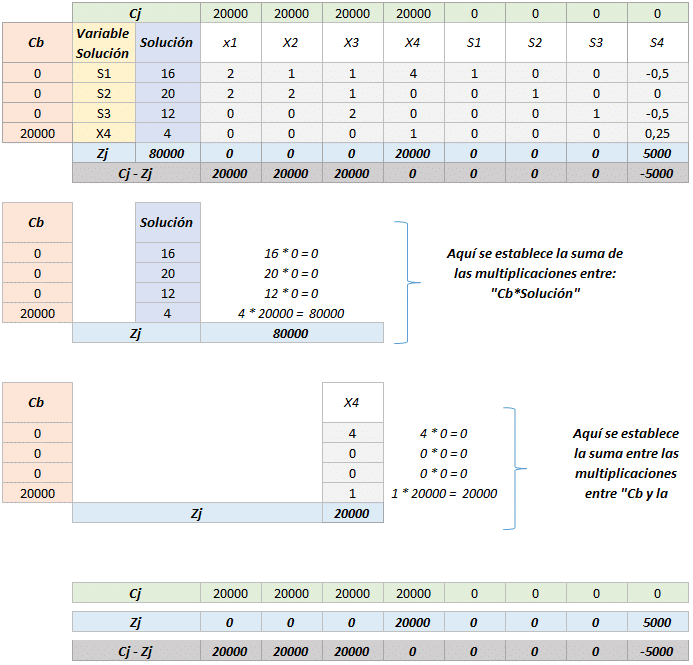
De esta manera se culmina la primera iteración, este paso se repetirá cuantas veces sea necesario y solo se dará por terminado el método según los siguientes criterios.
| Maximizar | Minimizar | |
| Solución Óptima | Cuando todos los Cj – Zj sean <= 0 | Cuando todos los Cj – Zj sean >= 0 |
- Continuamos con las iteraciones para lo cual tenemos que repetir los pasos anteriores.
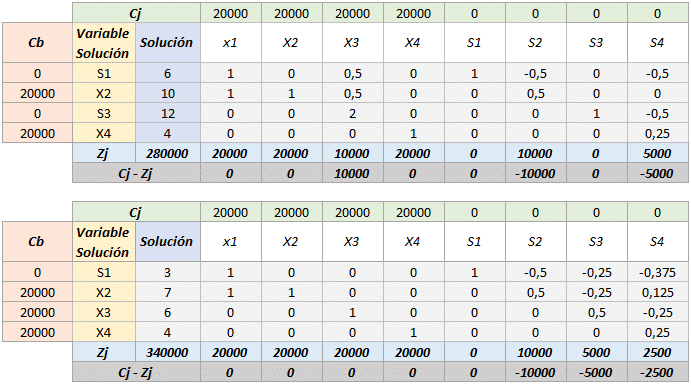
En esta última iteración podemos observar que se cumple con la consigna Cj – Zj <= 0, para ejercicios cuya función objetivo sea «Maximizar», por ende hemos llegado a la respuesta óptima.
X1 = 3
X2 = 4
X3 = 6
X4 = 4
Con una utilidad de: $ 340000
Sin embargo una vez finalizado el Método Simplex se debe observar una matriz identidad en el rectángulo determinado por las variables de decisión, el hecho de que en este caso no se muestre la matriz identidad significa que existe una solución óptima alterna.
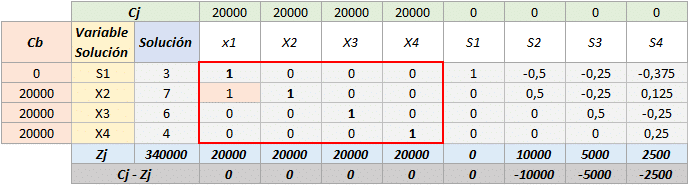
La manera de llegar a la otra solución consiste en alterar el orden en que cada una de las variables entró a la solución básica, recordemos que el proceso fue decidido al azar debido a la igualdad en el Cj – Zj del tabulado inicial. Aquí les presentamos una de las maneras de llegar a la otra solución.
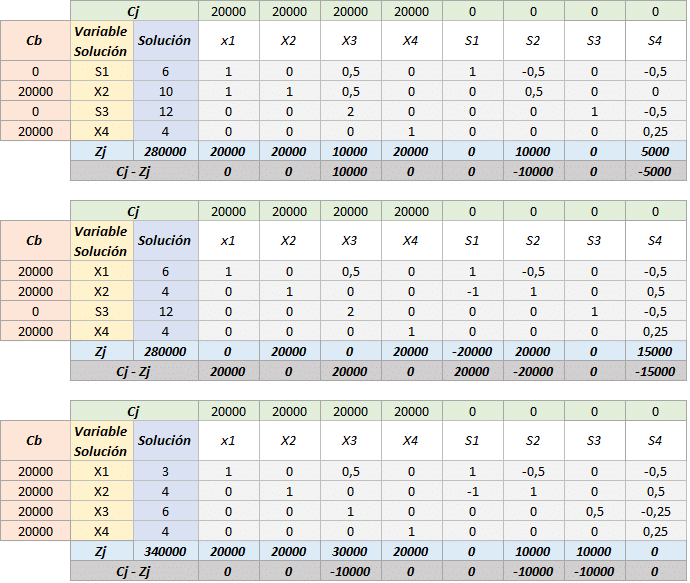
Podemos observar como existe una solución óptima alternativa en la cual la combinación de variables es distinta y existe un menor consumo de recursos, dado que el hecho de que se encuentre la variable «S1» en la solución óptima con un coeficiente de «3» significa que se presenta una holgura de 3 unidades del recurso (pieza rectangular de 8 pines).
X1 = 0 (Cantidad de mesas a producir = 0)
X2 = 7 (Cantidad de sillas a producir = 7)
X3 = 6 (Cantidad de camas a producir = 6)
X4 = 4 (Cantidad de bibliotecas a producir = 4)
S1 = 3 (Cantidad de piezas rectangulares de 8 pines sin utilizar =3)
Con una utilidad de: $ 340000
Problemas de minimización con el Método Simplex
Para resolver problemas de minimización mediante el algoritmo simplex existen dos procedimientos que se emplean con regularidad.
- El primero, que a mi juicio es el más recomendable se basa en un artificio aplicable al algoritmo fundamentado en la lógica matemática que dicta que «para cualquier función f(x), todo punto que minimice a f(x) maximizará también a – f(x)». Por lo tanto el procedimiento a aplicar es multiplicar por el factor negativo (-1) a toda la función objetivo.

A continuación se resuelve el algoritmo como un problema de maximización.
- El segundo procedimiento, el cual pretende conservar la minimización consiste en aplicar los criterios de decisión que hemos esbozado con anterioridad, en los casos de la variable que entra, que sale y el caso en el que la solución óptima es encontrada. Aquí recordamos los procedimientos según el criterio dado el caso «minimizar».

Solver es una herramienta que forma parte de una serie de comandos, a veces denominados de «análisis Y si». Con Solver, puede buscarse el valor óptimo para una fórmula de celda, denominada celda objetivo, en una hoja de cálculo.
Solver funciona en un grupo de celdas que estén relacionadas, directa o indirectamente, con la fórmula de la celda objetivo. Solver ajusta los valores en las celdas cambiantes que se especifiquen, denominadas celdas ajustables, para generar el resultado especificado en la fórmula de la celda objetivo.
Pueden aplicarse restricciones para restringir los valores que puede utilizar Solver en el modelo y las restricciones pueden hacer referencia a otras celdas a las que afecte la fórmula de la celda objetivo, lo cual lo constituyen en una herramienta adecuada para solucionar problemas de programación lineal, y programación lineal entera.
Algoritmos y métodos utilizados por Solver
La herramienta Microsoft Excel Solver utiliza el código de optimización no lineal (GRG2) desarrollado por la Universidad Leon Lasdon de Austin (Texas) y la Universidad Allan Waren (Cleveland).
Los problemas lineales y enteros utilizan el Método Simplex con límites en las variables y el método de ramificación y límite (método de branch and bound), implantado por John Watson y Dan Fylstra de Frontline Systems, Inc. El método de branch and bound corresponde al mismo método utilizado por WinQSB para la solución de problemas de programación lineal entera y/o que utilicen variables binarias.
¿Cómo habilitar el complemento Solver de Excel?
Microsoft Office 2010
El primer paso consiste en dirigirse a la pestaña Archivo, dirigirse a la opción Ayuda y seleccionar la opción Opciones:

Luego, se abrirá una ventana emergente de Opciones de Excel, en ella vamos a la opción Complementos (ubicada en la barra lateral izquierda). Ya en complementos, nos dirigimos a la opción Administrar: Complementos de Excel y damos clic en botón Ir:

Luego se abrirá una pequeña ventana emergente, en ella se podrán observar varios complementos junto con una casilla de verificación cada uno. Activamos la casilla de verificación de Solver y damos clic en Aceptar:

Una vez se ha habilitado el complemento, Solver se ubicará en la pestaña de Datos.
Solución de un problema de programación lineal mediante Solver
Al igual que para cualquier otro método de resolución, el primer paso para resolver un problema de programación lineal (PL) consiste en el modelamiento matemático, y es en esta fase en la que el profesional de Ingeniería Industrial debe desarrollar su mayor habilidad y destreza. Los pasos para resolver un problema de PL se encuentran en el módulo de programación lineal. Sin embargo, dada la interfaz de Excel, el modelamiento se hace más simple, siempre y cuando nos caractericemos por organizar muy bien la información.
El problema

Declaración de variables
x = Cantidad de bicicletas de paseo a producir
y = Cantidad de bicicletas de montaña a producir
Restricciones de capacidad
Aluminio:
x + 2y <= 80
Acero:
3x + 2y <= 120
Función Objetivo
Zmax = 20000x + 15000y
Ingresando los datos a Excel
Tal cómo se mencionó, la importancia de una correcta organización de la información es vital, proponemos la siguiente plantilla para ingresar los datos de nuestro problema:

El siguiente paso corresponde a registrar la información en la plantilla, de acuerdo a los datos que tenemos en el problema:

El siguiente paso consiste en formular la plantilla, para ello debemos considerar ¿qué pasaría si cambiaran las variables de decisión? Pues, en caso tal de que las variables sufrieran cambios se alteraría la contribución total, y el inventario de recursos. Por ello, debemos formular en consecuencia:

Ahora que ya tenemos nuestra plantilla formulada, el siguiente paso consiste en utilizar Solver para resolver el modelo, para ello, vamos a la pestaña Datos (En cualquier versión de Office), y seleccionamos el complemento Solver:

Una vez iniciemos Solver se abrirá una ventana emergente llamada Parámetros de Solver, en ella como primera medida seleccionaremos nuestra celda objetivo (Contribución Total) y seleccionaremos el criterio Maximizar:

El siguiente paso, es indicarle a Solver que debe alcanzar el máximo valor para la celda objetivo mediante la variación de las siguientes celdas (Cambiando las celdas), es decir, le indicaremos cuales son las variables de decisión:



El siguiente paso consiste en asignarle las restricciones a las que el modelo está sujeto, las cuales son restricciones de disponibilidad de recursos:


Lo que nos muestra la imagen anterior es la forma de indicarle la restricción a Solver, para que el inventario usado sea menor o igual al inventario disponible. De igual forma debe hacerse para el recurso de Aluminio.

La siguiente restricción es la de no negatividad, es decir, que las variables de decisión no puedan tomar valores menores que cero.

Si quisiéramos resolver el modelo tal cual como está pudiésemos hacerlo, y obtendríamos quizá una respuesta que distaría de su aplicación práctica, dado que es probable que la respuesta nos de variables continuas, y en la práctica vender 0,6 bicicletas es un poco complicado. Por tal razón, agregaremos una restricción que hace que el ejercicio se resuelva mediante programación lineal entera, indicando que las variables de decisión deban ser enteras:

Hecho esto, damos clic en Aceptar y en Resolver… Podemos observar como las variables de decisión, las restricciones (inventario usado) y la contribución total (celda objetivo) han tomado valores, estos son los valores óptimos según el modelo formulado. Ahora nos aparecerá un cuadro de diálogo que nos preguntará si deseamos utilizar la solución de Solver y unos informes que debemos seleccionar para obtener una tabla resumen de la respuesta y un análisis de sensibilidad que se insertarán como hojas al archivo de Excel:

El informe de sensibilidad arrojado por Solver es mucho más básico que el que nos puede proporcionar WinQSB, sin embargo destacamos la información referente al «Multiplicador de Lagrange» que corresponde al «Shadow Price de WinQSB» conocido como el precio sombra, es decir, el cambio marginal de la función objetivo cuando el valor del lado derecho de la restricción aumenta en una unidad, en este caso, por cada kg de Acero adicional que dispongamos, la función objetivo aumentaría en $ 1250.

Este mismo ejercicio fue resuelto con WinQSB y TORA arrojando iguales resultados, el archivo de Excel utilizado para esta demostración se adjuntará a continuación para su descarga:
Interpretación del Informe de Sensibilidad de Restricciones de Solver
Continuando con el Análisis de Sensibilidad (o Análisis Postoptimal) en la resolución de modelos de Programación Lineal, se muestra la interpretación del Informe de Sensibilidad (o Informe de Confidencialidad en algunas de las versiones de Office que datan del año 2010 a la fecha) de restricciones de Solver, comúnmente conocido como el análisis del Precio Sombra de cada una de las restricciones.
Por ejemplo, la versión de Solver disponible con Office 365 ofrece la siguiente interfaz para obtener el Informe de Sensibilidad (luego de alcanzar la solución óptima del problema en su escenario base).
En el caso de la versión de Solver compatible con Office 2007 y Office 2003, la interfaz es la siguiente:
De modo de ilustrar su correcta interpretación, a continuación consideraremos nuevamente nuestro ejemplo de Programación Lineal:
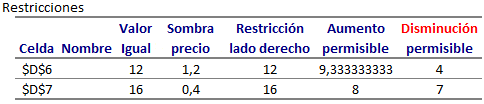
Con solución óptima X=14/5 Y=8/5 y valor óptimo V(P)=20,8. El Informe de Restricciones de Solver corresponde a:
Las filas del Informe de Restricciones corresponden a las restricciones 1 y 2, respectivamente.
En el caso de la restricción 1 el Precio Sombra es de 1,2 y el valor de la restricción (lado derecho) es igual a 12. Para dicho parámetro (lado derecho) se permite un aumento de de 9,33 y una disminución de 4, es decir, el lado derecho de la restricción 1 puede variar entre [8, 21,33] (12-4, 12+9,33) y el Precio Sombra de magnitud 1,2 seguirá siendo válido (es decir, se conserva la base óptima).
Esto significa que si, por ejemplo, el lado derecho de la restricción 1 aumenta en 1 unidad y el resto de los parámetros del modelo permanecen constantes, el nuevo valor óptimo será: V(P)=20,8+1*1,2=22.
Ahora bien, si por ejemplo, el lado derecho de la restricción 1 disminuye a 10 el nuevo valor óptimo será: V(P)=20,8-2*1,2=18,4.
Finalmente si la variación del lado derecho esta fuera del intervalo [8, 21,33] NO se puede utilizar el Precio Sombra para poder predecir cuál será el nuevo valor óptimo. Esto se debe a que la nueva solución óptima ya no se encontrará con las mismas restricciones activas, es decir, cambia la base óptima.
De forma análoga, para la restricción 2 el Precio Sombra es de 0,4 y este valor es válido si su lado derecho varía entre [9, 24] (16-7, 16+8). Por ejemplo, si el lado derecho de la restricción 2 aumenta en 3 unidades (y el resto de los parámetros permanece constante) el nuevo valor óptimo será: V(P)=20,8+3*0,4=22.



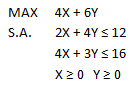

Comentarios
Publicar un comentario